벡터 ( vector )
크기와 방향을 모두 가진 물리량을 벡터( vector )라고 한다.
합성 벡터
한 지점에서 두 물리량을 결합시켜 얻은 결과를 합성 벡터라고 하고 두 벡터의 합( sum )이라 한다.
평행사변형 법칙 ( parallelogram law )
두 벡터를 결합시키는 규칙을 벡터 합( sum )의 평행사변형 법칙이라 한다.
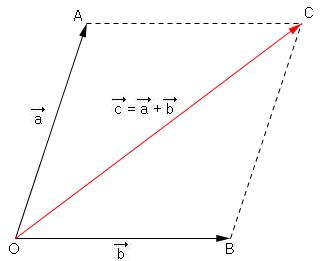
시점이 원점으로 일치하는 두 벡터 a,b의 합은 원점에서 시작하는 벡터이고, 이를 a와 b를 이웃한 변으로 하는 평행사변형의 대각선으로 나타낸다.
여기서 a, b 중에 어느 것을 먼저 택하고 어느 것을 처음 벡터의 종점으로 이어 붙일지 그 순서는 중요하지 않다.
( = 교환 법칙 ) a + b = b + a 이 성립
더보기
속도 ( velocity ) : 크기와 방향을 모두 가진 물리량
속력 ( speed ) : 방향을 무시한 속도의 크기만을 나타낸 단위
스칼라 곱 ( scalar multiplication )
벡터는 크기를 확대하거나 축소할 수 있다. 벡터에 실수를 곱하는걸 스칼라 곱이라 한다.
유향 선분
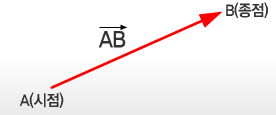
선분에 방향을 나타내는 것을 뜻한다.
벡터 공간( vector space ) : 벡터 합과 스칼라 곱의 대수적 성질 8가지
- 모든 벡터 x, y에 대해서 x + y = y + x 이다.
- 모든 벡터 x, y, z에 대하여 ( x + y ) + z = x + ( y + z ) 이다.
- 모든 벡터 x에 대하여 x + 0 = x 를 만족하는 벡터 0이 존재한다.
- 각 벡터 x 마다 x + y = 0 을 만족하는 벡터 y가 존재한다.
- 모든 벡터 x에 대하여 1x = x 이다.
- 모든 실수 a, b와 모든 벡터 x에 대하여 ( ab )x = a( bx )이다.
- 모든 실수 a와 모든 벡터 x, y에 대하여 a( x + y ) = ax + ay 이다.
- 모든 실수 a, b와 모든 벡터 x에 대하여 ( a + b )x = ax + bx 이다.
2차원 평면 뿐 아니라 3차원 공간에서도 8가지 성질을 만족한다. 이 결과는 공간에서 직선의 방정식과 평면의 방정식을 나타내는데 사용된다.
직선의 방정식
( 단, t는 임의의 실수이고 x는 직선 위 임의의 점 )
평면의 방정식
( 단, s, t는 임의의 실수이고 x는 평면 위 임의의 점 )
'과거 자료' 카테고리의 다른 글
| 뷰 포트 시점을 객체에 고정 하기 (0) | 2022.10.26 |
|---|---|
| [#3] 회전 변환 식 유도하기 (0) | 2022.10.25 |
| 이미지를 회전, 확대 및 축소, 대칭 이동하기 (0) | 2022.10.08 |
| [#2] 삼각함수 공식 정리 (0) | 2022.09.21 |
| [#1] 역삼각함수 - arcsin, arccos, arctan (0) | 2022.09.17 |
